Luck is a frequent topic of discussion among gamers. When we lose, we accuse the victors of getting lucky. When discussing our opinions about games, we might claim that “that game is all luck,” or “I like a game with a fair amount of luck.” There are a lot of connotations wound up with the word luck – we tend to associate it with things like dice, which produce outcomes which are outside of our control. We may also view a win attributed to luck as dishonorable or undeserved, as opposed to a well earned win attributed to a clever show of skill. But sometimes these attributions are not so straightforward. In a bluffing game, I might claim that “you’re luck y I didn’t call,” but you would protest claiming that “it was all skill.” If we are to settle these disagreements, which are of course of the utmost importance, we have to carefully define our terms. I think it’s useful to formalize the way we talk about luck and skill in games, so that it is easier to discuss rather complex topics having to do with games while minimizing discussion of semantics.
y I didn’t call,” but you would protest claiming that “it was all skill.” If we are to settle these disagreements, which are of course of the utmost importance, we have to carefully define our terms. I think it’s useful to formalize the way we talk about luck and skill in games, so that it is easier to discuss rather complex topics having to do with games while minimizing discussion of semantics.
Many of the ideas that follow are not mine, but instead come from game theory, talks and writing by Richard Garfield, and the book Characteristics of Games by George Skaff Elias, Karl Robert Gutschera, and Richard Garfield. I try to use terminology which is consistent with these writers, while expounding upon their ideas.
An important preliminary point I must make, which is tho roughly discussed in Characteristics of Games is that luck and skill are not opposites. Sometimes people will call games “luck-based” in contrast with games which are “skill-based,” but these are poor classifications. In fact, luck and skill can coexist in a game in any combination of levels. Some classic examples are: Texas Hold’em is a game with high skill and high luck; Chess is a game with high skill and low luck; Sorry! is a game with high luck and low skill, and Tic-Tac-Toe is a game with low luck and low skill. Nonetheless, in order to talk about luck, we have to talk about skill, and vice versa.
roughly discussed in Characteristics of Games is that luck and skill are not opposites. Sometimes people will call games “luck-based” in contrast with games which are “skill-based,” but these are poor classifications. In fact, luck and skill can coexist in a game in any combination of levels. Some classic examples are: Texas Hold’em is a game with high skill and high luck; Chess is a game with high skill and low luck; Sorry! is a game with high luck and low skill, and Tic-Tac-Toe is a game with low luck and low skill. Nonetheless, in order to talk about luck, we have to talk about skill, and vice versa.
Actually, for now I will avoid talking about “luck” and instead talk about “randomness” or “indeterminacy.” “Luck” is a word loaded with connotations – “randomness” is too, but perhaps less so. Later on, I will talk about a possible formal definition for the word “luck.”
Randomness is Abstract
Randomness is a way of modeling uncertainty. In mathematics, a deterministic function is one for which the outcome can be predicted with 100% accuracy if we know the input. A random function is one for which even if we know the input, we can’t fully predict the outcome. Instead, we can only characterize the outcome as a probability distribution; it may be more likely to take on one value than another, but we can’t be 100% sure which value it will take. Ignoring for now quantum mechanics, which I’m fairly certain has little impact on the analysis of board games, the real world is deterministic, but extremely complicated.
Therefore we use randomness to model complicated things in the real world to compensate fo r the fact that we will never be able to fully account for every causal factor, and thus we know there will be some error in our model’s predictions. Randomness is just a way of modeling uncertainty, which is why it is synonymous with “indeterminacy.” If we can’t fully determine the outcome, then we can interpret the outcome to be random.
r the fact that we will never be able to fully account for every causal factor, and thus we know there will be some error in our model’s predictions. Randomness is just a way of modeling uncertainty, which is why it is synonymous with “indeterminacy.” If we can’t fully determine the outcome, then we can interpret the outcome to be random.
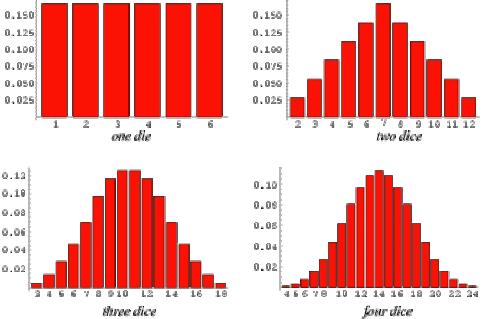
A common misunderstanding about randomness has to do with the fact that we may have a lot of information about something but still interpret it using randomness. Often when we use the word “random,” people interpret it to mean “completely at random,” or “uniformly at random,” which is just one possible distribution we can use to model things. When we roll a six-sided die, the result is uniformly random with equal probabilities associated with each number one through six. When we roll two dice and sum the results, the outcome is no longer uniformly distributed, as most gamers know. The most likely outcome is 7 with a probability of 1/6, while there is only a 1/36 chance of rolling a 12. Even though the distribution is not “uniformly” random, the outcome is just as random as rolling a single die, even though the distribution isn’t uniform. A competent Catan player can use their knowledge of the non-uniform distribution of the die rolls to make better decisions than an imbecile, but the outcome of the die rolls is still random.
However, we may call something “more random” or “less random,” which is actually a slightly confusing and inconsistent way of talking about particular random distributions. When we say “more random,” sometimes we mean that the random distribution we are using to model an outcome has a higher “variance,” which means that values we may observe are more spread out, or we might say “more random” to refer to a distribution that is closer to a uniform distribution. For now, I will avoid these terms.
Now I will make the contentious claim that nearly all games have randomness, including games often thought of as “zero-luck” such as Chess and Terra Mystica. We can prove that there is randomness in Chess by looking at the outcomes of the games. Often in tournaments, we will see a player with a lower rating beat a player with a higher rating. There are two factors which could contribute to this: we have some uncertainty about what the true rating of the players should be, so the outcome of this match may be evidence that their rating should be adjusted, but also this match could just be anomalous. Actually, the ratings (although the ELO rating system can be improved upon greatly) are designed to have the following interpretation: the outcome of a game of chess is a random function of the difference between the players’ skill levels. If a 1700-rated  player plays a 1600-rated player, the 1700-rated player should win about 2/3 of the time. We directly observe indeterminacy in the outcome of the matches – we model the outcomes using randomness.
player plays a 1600-rated player, the 1700-rated player should win about 2/3 of the time. We directly observe indeterminacy in the outcome of the matches – we model the outcomes using randomness.
Many gamers object to this use of the word “random.” They claim that the outcome of the game is not random, because we can look back and understand deterministically what moves led to the outcome of match. But randomness is a function of perspective. Before we observe the way the match unfolds, our predictions about the outcome of the match are subject to uncertainty, and we can characterize this uncertainty with a probability distribution. The nature of the random component depends entirely on one’s frame of reference; before the match, we have a certain amount of uncertainty about the outcome. Halfway through the match, we may have a different level of uncertainty about the outcome of the match, depending on the board state.
Three Types of Randomness in Games
Where does this uncertainty come from in Chess and in other games? The most useful and consistent way I have found of categorizing randomness in games comes from game designer Richard Garfield, although I will try to expound upon his ideas. According to Garfield, there are three sources of indeterminacy in games.
“Type I” randomness is the most familiar – it is the type of randomness which arises from mechanical randomizers in a game, such as die rolls or random card draws from a deck. Generally, I find players are comfortable calling this kind of randomness “luck,” as in “lucky rolls” or “lucky draws.” Everyone I have met is comfortable calling these outcomes random despite the fact that technically die rolls could be predicted with 100% accuracy if we knew enough about the physical forces acting on the die as it were rolled. Card draws, too, could be predicted accurately if we knew enough about the exact permutations applied to the deck of cards as it were shuffled. These game elements should certainly be considered “random,” but we should recognize that technically this randomness arises from our limitations as humans. The randomness is a way of modeling our uncertainty which arises from something very complex – in this case, physics.
“Type II” randomness is the indeterminacy which arises from hidden information and simultaneous decision making. For instance, the existence of hidden roles in a game often means that the outcome of a player’s decision will be unknown to her as she makes it. In games with simultaneous decision making, there is an overt randomness built into the strategic decision making. This is contentious – I find that often players feel that simultaneous decision making cannot be considered random because players have complete control over their strategic cho ices. However, a game theoretical analysis of simple games with simultaneous decision
ices. However, a game theoretical analysis of simple games with simultaneous decision
making, called “Von Neumann games” yields the perhaps counterintuitive result that in some games, the best decisions should be made randomly. (Remember, this does not mean ‘uniformly at random,’ but rather, ‘according to some probability distribution’).
A Von Neumann game (named after an eminent game theorist and otherwise genius) is one in which players each make a simultaneous decision, and the payoff to each player depends on the decisions made by all players. For instance, The Prisoner’s Dilemma is a Von Neumann game, as is Rock Paper Scissors. Two-player Von Neumann games can be modeled using a matrix – each cell of the matrix has a number which represents the payoff to each player that would result in Player 1 choosing the corresponding row and Player 2 choosing the corresponding column. Depending on the mathematical properties of that matrix, we can find the optimal strategies for each player. In The Prisoner’s Dilemma, depending on the payoffs, the optimal strategy is to choose to betray your opponent 100% of the time, so there is not necessarily any randomness built into the strategy. But in Rock Paper Scissors, choosing one option 100% of the time is clearly suboptimal, because your opponent will simply choose the option which counters yours. Therefore, you will have to choose your moves in Rock Paper Scissors in a non-deterministic fashion; theoretically, if you were choosing your moves according to a deterministic function, your opponent could also use that information to counter you. (The game theoretically equilibrium -optimal and common sense strategy is to choose each option at random with probability 1/3, although in some cases you may be able to do better by exploiting determinism in your opponents moves).
-optimal and common sense strategy is to choose each option at random with probability 1/3, although in some cases you may be able to do better by exploiting determinism in your opponents moves).
Of course modern board games are much more complex than simple Von Neumann games, but small parts of games with simultaneous decision making can be modeled as Von Neumann games, for instance, simultaneous action selection. When players must make simultaneous decisions, there is usually some incentive to be unpredictable, so that opponents cannot take advantage of your choices. Part of the strategy of the game will be choosing the probability distribution with which a player makes his choices, which is illustrative of the fact that skill and randomness can coexist and interact, but the existence of skill does not erase the contribution of randomness to these scenarios.
“Type III” randomness is the most abstract and pushes the boundary of what most people are willing to consider randomness. This is the type of indeterminacy which arises from player limitations. In game theory, we generally study optimal strategies, which can only be found for relatively simple games. Any game worth playing, however, will be outside of the realm of solvability. Even though modern AIs can beat humans at Chess and Go, and by extension probably every modern board game if enough money were thrown into their development, this is a far cry from actually “solving” a game. So on top of the fact that even simple, solved games played by two perfect players can have uncertain outcomes due to mechanical (Type I) randomness and hidden information (Type II), the reality is that all of us are playing games sub-optimally. Because in Chess there is no Type I or Type II randomness, this is the only way to explain the indeterminacy in the outcomes of games of Chess.
The game of Chess can be modeled as an enormous game tree, wherein White’s first move is represented by 20 branches (as there are 20 possible opening moves), then each of those branches splits into 20 additional branches representing each of Black’s possible opening moves, and so on. Obviously this game tree quickly becomes unfathomably enormous, and the game cannot realistically be analyzed by following every branch to its conclusion. Therefore, in playing the games we have to use incomplete, sub-optimal analyses called “heuristics” to guide our decision making. Inevitably, in playing chess, we are forced to make decisions which have consequences we cannot fully predict. According to some heuristics, two moves may be indistinguishable in quality, but of course the outcome of the game may be different depending on which decision is made. This partially explains why if two players play several games of chess, the winner may change from game to game. The complicated heuristics of the two players interact in even more complicated ways, in a realm which is beyond our calculations. This can be compared to the way when we roll a die, the forces act on the die in ways we cannot fully account for, resulting in a random outcome. It is difficult for us to feel subjectively the same way about Type I and Type III randomness, because in Type III randomness, there is no obvious departure from human agency.
I do believe that any game with indeterminacy in outcome must have at least one of these three types of randomness. However, some sources of randomness in games do not fit perfectly into any of these three categories, but rather emerge from the interaction of these types of randomness. A prominent source of randomness that exists in most modern multiplayer (i.e. more than two-player) games is the indeterminacy which can arise from player interaction. To be clear, player interaction is not necessarily a source of randomness – if all players were playing a simple game using strategies that were fully optimal, a perfect player would be fully aware of the strategies of all other players, and could make decisions that were sensitive to those other players’ possibly deterministic actions. Realistically, however, games are too complex for players to use truly optimal strategies, and thus it is impossible to for one player to know exactly what strategies the other players will be using. Therefore, the sub-optimal strategies of players can be considered information which is hidden from other players. In a way, this is Type II randomness, because the indeterminacy is the result of hidden information, but the information is hidden because of our limitations as players to formulate optimal strategies. I like to call this “Type 2.5” randomness, because it lies at the intersection of Type II and Type III randomness.

Strategy and Skill
There is a difference between the way we tend to use the word “strategy” when talking about modern games and the game theoretical definition. Informally, we tend to use strategy to talk about specialization in modern games, as in “I’m using the sheep trading strategy” or “my strategy is to stay in my own corner of the map and not make anyone angry.” Many people have written about using strategy in this context, and especially the relationship between strategy and tactics. The game theoretical use of “strategy” is more general, and considerably more abstract when applied to modern games. When applied to games like Rock Paper Scissors, a strategy is something like “choose Rock, Paper or Scissors with probability 1/3.” More generally, a player’s strategy is a move-generating function which takes the current game state and spits out a decision. It is even possible (and in fact likely, for reasons discussed above) for strategies to include random decisions, such as “when you decide which combat card to play face down, choose ‘run away’ with probability 1/3 or ‘parry’ with probability 2/3, unless the opponent has more than 5 troops, in which case choose ‘run away’ with probability 2/3 and ‘parry’ with probability 1/3.”
Therefore, a strategy in this sense probably doesn’t really exist, because no player has actually considered what they would do and what probabilities they would use in every possible situation given every possible board state. Players generally make up their mind as they go, even acting inconsistently (especially in games which require dexterity)! However, we could imagine very abstractly that the random choices in a strategy could include even those variations caused by inconsistency in the behavior of the player. This is getting quite far from our normal usage of the word “strategy.” Nonetheless, strategy in the game theoretical sense is a useful concept, if abstract, because it will help me talk about skill and luck. When I refer to a player’s strategy, I am referring to the notion of what that player would do in every possible situation, even though we couldn’t realistically explicitly observe a strategy.
Skill, then, is related to a strategy. I believe our common usage of skill is that “level of skill” is a measurement of the quality of a player’s strategy. How sophisticated is the player’s strategy? How finely tuned are its parameters? Most importantly, how does a strategy fare against the other strategies in the space of strategies? Thus skill is a low-dimensional (often 1-dimensional) summary of the extremely complicated mathematical object which is a “strategy.” Furthermore, measuring skill is a difficult task; if we are to do so empirically by observing the outcomes of games, it becomes hopelessly confounded with the impact of randomness on the game. If Player 1 beats Player 2 55% of the time, is this because Player 1 has a much higher level of skill but there is a lot of randomness, or is this because Player 1 is only slightly better than Player 2? In order to measure the amount of randomness in a game, as I will discuss, depends on the skill levels of the players, so it’s a vicious cycle. In order to measure either one, we will have to make certain assumptions about the distribution of skills of the player or about the amount of randomness in the game. (Current rating systems like the Bradley Terry model, Microsoft TrueSkill and ELO fix an arbitrary value representing the amount of luck in the game in order to assign skill ratings to players). I hope to pin down a better way of thinking about skill in the future, but for now I am mostly concerned with defining “luck”.
Luck in Theory
I have hopefully established, at the very least, that there randomness in all of the games we play, and that some things are random even if they are also highly skill dependent, even if they don’t involve dice or cards. Here I will try to reincorporate the loaded word “luck” into the discussion of randomness in games. Ordinarily, I think luck is used to refer to Type I randomness, but I think calling Type I randomness luck at the exclusion of Type II and III luck is inconsistent. Fundamentally, all three types of randomness are the result of decision making under uncertainty. However, outcomes which are highly dependent on a player’s strategy are generally not considered to have very much luck.

I propose that the amount of luck in an outcome of a game is the degree of indeterminacy in that outcome after accounting for the players’ strategies. In mathematical terms, luck is the variance of the outcome of a game conditional on the players’ strategies. If, considering the move-generation function of each player, there is 100% certainty that he will achieve a certain outcome to an observer who is aware of all players’ strategies, then there is no luck in that outcome for that player. Otherwise, whether or not that objective is accomplished is partially a matter of luck, and the degree of luck depends on the distribution of outcomes. A game with a lot of luck is one in which, conditional on the players’ strategies, the winner is still highly uncertain.
If luck is defined with respect to players’ strategies, clearly the amount of luck in a game depends on who is playing it. This is a positive feature of the definition, because as I discussed in the context of chess, the amount of chaos and unpredictability in a game often increases as skill levels decrease. If we were interested in ascertaining a single number which described the amount of luck in a game, we would lose a lot of information, but we could do so averaging out the amount of luck in games with players of every different possible strategy, perhaps weighted by the prevalence of that strategy in the population of players. Because strategies themselves are too complex to explicitly express, and the prevalence of strategies can never be known, this idea is purely theoretical.
It is worth noting that if we are defining luck as the variance of an outcome conditioning on players’ strategies, only certain types of randomness are included in luck. All Type I randomness is included, because Type I randomizers are exogenous to a players’ strategy. Furthermore, most Type II randomness is realized through randomized or probabilistic strategic choices, so it would also be captured by this definition of luck. Some Type III randomness is also included, for instance when our limitations as players cause us to make arbitrary or indifferent choices. (Google’s Go-playing AI AlphaGo uses a random number generator to perform a “stochastic search” of the game tree. Perhaps human brains can be viewed as using similarly random processes). However, if we make systematically sub-optimal choices which are unpredictable to other players, this would not be considered to be a source of luck. Conditioning on strategy means that we would already be taking these choices into account when predicting the outcome of the game.
In practice, we are resigned to working with “skill level” as a summary of a player’s strategy. The relationship between luck and skill level is a little bit more complex. Mathematically, the quantity “the variance in the outcome of a game conditional on the players’ skill levels,” is guaranteed to be higher than the amount of luck in a game as I have defined it above. This is because the variance of the outcome of the game will include not just the variance due to luck, but also variance due to the loss of information when we collapse “strategy” into “skill.” However, by making assumptions about the way strategies might vary within individual skill levels, we may still productively use skill as a proxy for strategy in the measurement of luck.
 The amount of luck in a game can be considered to be luck in the final outcome of the game. In all games, the greater the difference between the level of skill of the players, the greater the probability that the more skilled player will win. In a game with a large amount of luck, a large difference in player skill may only result in moderately unequal odds of winning. In a game with a small amount of luck, a small difference in player skill may result in highly unequal odds of winning.
The amount of luck in a game can be considered to be luck in the final outcome of the game. In all games, the greater the difference between the level of skill of the players, the greater the probability that the more skilled player will win. In a game with a large amount of luck, a large difference in player skill may only result in moderately unequal odds of winning. In a game with a small amount of luck, a small difference in player skill may result in highly unequal odds of winning.
New players will regularly beat experienced players at Can’t Stop, which is a good indicator that Can’t Stop is a game with a lot of luck. However, new players will very rarely beat experienced players at Chess or Agricola, which is a good indication that there is less luck in those games.
The problem of empirically measuring the amount of luck in a game is an interesting problem for which I have not yet come across a satisfactory solution. However, I believe that the above is a reasonable definition for luck which is as consistent as possible with common usage and (theoretically) measurable.
Luck in Practice
Wound up in this definition of “luck” are concepts including randomness as indeterminacy, theoretical constructs like “strategy,” and concepts from probability like “conditionality.” This can make it difficult to talk about. Nonetheless, I feel all of these components are necessary to get an accurate definition for luck that can help provide a framework for discussions about the luck content of modern board games. Using this definition, I can provide some examples of elements in games that can contribute to increasing the amount of luck in games.
Obviously, die rolls and card draws tend to decrease the degree to which outcomes in
games are dependent on strategic choices. Having said that, it’s possible for a game with frequent die rolling to actually have less luck than a game with rare die rolling. Over a large number of die rolls, the average results will converge towards a predictable quantity. What matters is unpredictability of outcomes that results from this die rolling. If individual die rolls cause significant changes in the game state that put some players at a great disadvantage, then this part of the game can be considered to be significantly luck-based. If, however, frequent die rolls modify values slightly, such that the progression of the game remains mostly predictable with only small upsets, then the contribution of the dice to the amount of luck in the game could be considered small. This illustrates how it can be difficult to try to fully characterize the amount of luck by simply tallying the randomness-generating components; in order to quantify the amount of luck in the game, we have to look at the uncertainty in the outcomes.
Generally, the more complicated a game is, the more indeterminacy there is in the outcome with respect to players’ strategies. Here, “complicated” refers to how difficult it is for players to develop heuristics. A game might have one thousand components and a 50 page rulebook, but if it is immediately obvious to all players what moves need to be made to optimize their outcomes, the game is not really very complex. Therefore, for more complex games, it is more difficult to develop strategies, and the winner is more likely serendipitous. One can imagine two complete novices playing Go, each working with some rudimentary heuristics that they have invented, but without the necessary experience for their heuristics to be meaningful. In this example, these players’ strategic choices will have a relatively low impact on their chances of winning. This is an extreme example, but the concept applies to all games – due to Type III randomness, the complexity of a game can contribute to the amount of luck.
The contribution of simultaneous decision making and the resultant Von Neumann type randomness to the amount of luck in games is, I feel, greatly underestimated. In fact, it seems that game designers can include blind bidding and simultaneous action selection in games with impunity, avoiding criticism from those gamers who otherwise detest randomizers such as dice. The description on the front cover of “Food Chain Magnate” brashly advertises “100% Dice Free… There is no such thing as luck. Skill wins every time,” despite the fact that it is partially a game of simultaneous action selection. Jamey Stegmaier claims, in his blurb about his new game “Scythe” that “Combat is driven by choices, not luck or randomness” despite the fact that combat in Scythe is based on simultaneous card selection and blind bidding.
resultant Von Neumann type randomness to the amount of luck in games is, I feel, greatly underestimated. In fact, it seems that game designers can include blind bidding and simultaneous action selection in games with impunity, avoiding criticism from those gamers who otherwise detest randomizers such as dice. The description on the front cover of “Food Chain Magnate” brashly advertises “100% Dice Free… There is no such thing as luck. Skill wins every time,” despite the fact that it is partially a game of simultaneous action selection. Jamey Stegmaier claims, in his blurb about his new game “Scythe” that “Combat is driven by choices, not luck or randomness” despite the fact that combat in Scythe is based on simultaneous card selection and blind bidding.

But even the simultaneous decision making in these games likely does not contribute to the indeterminacy in the outcomes as much as the simple fact that they are multiplayer games in which the unpredictable actions of one player can have large effects on another player in ways which are never fully in either player’s control. The authors of Characteristics of Games talk at lengths about the unexpected and often undesirable properties that emerge from multiplayer games in which players can target other players, either intentionally or inadvertently. This topic also fascinates me so I will hopefully write more about it in the future. For now, it suffices to say that an increased player count can contribute to an increased indeterminacy of outcomes to a degree which depends on the nature of the interaction allowed between players. I believe that games which carefully limit player interaction (and which are often accused of being “multi-player solitaire”) tend to have less luck than those which do not, all else being equal.
Conclusion
All of the examples I have just given are subject to scrutiny; perhaps the contribution of various types of randomness to the amount of luck in the game is larger or smaller than I posit. Due to the sophistication and complexity of modern games, I don’t think the amount of luck could ever be quantified by a theoretical analysis of the content of a game. Instead, we must use an empirical analysis of the outcome of games (win-loss data) to make inferences about the amount of luck in games. These inferences could help inform our understanding of the elements which make up these games. The complexity of modern board games cannot quite be compared to the complexity of most naturally occurring phenomena, but I believe it is necessary to use empiricism in conjunction with theory to understand them. I will hopefully write more about this later.
My main goal in this discussion is to convince readers to generalize their definition of luck so that it will include aspects of games that are partially the result of human agency, or partially predictable. I believe accepting that, for instance, simultaneous decision making can be a source of luck will help inform our analysis of games. I personally feel misled by claims that a game is highly serious and “no-luck” when in fact due to partially-agential randomizers, I feel like I have very little control over the outcome of a game. Meanwhile, I am perfectly willing to enjoy games which have a high degree of mechanical Type I luck depending on what the experience has to offer. Hopefully I have encouraged readers to see that luck can result from many factors including dice, cards, hidden roles, blind bidding, player interaction, or irreducibly complex circumstances, and of course the interactions between these factors.

nice article. enjoyed the read. keep them coming please!
LikeLike
This is exactly a type of piece I want to read on boardgames. I am certainly looking forward to your new posts!
LikeLike