In Part 1, I discuss growth in games and the definition of an engine building game. In Part 2, I discuss the problem of diverging player odds, odds diagrams, and the first of five solutions.
In Part 3, I discuss the remaining four solutions to the problem of diverging player odds:
- Damping Mechanisms (which coerce player standings into similarity)
- Variance Reduction Mechanisms (which reduce variation in player’s individual outcomes)
- Escalation (which delays the divergence of player odds)
- Obfuscation Mechanisms (which obscure logical player elimination).
These latter four solutions are general solutions to the problem of diverging player odds which are not specific to exponential games. However, exponential games may me more likely to feature these solutions due to their pathological diverging player odds.
Solution 2: Damping
We have gone over many ways that games decrease the magnitude of player growth. But reducing this amplification factor may not always be the best solution to the problem of diverging player odds, because it can undermine some of the desirable aspects of engine-building games, especially the ever-satisfying experience of becoming much more powerful over the course of the game. In order to retain reasonably slow divergence of player odds while allowing players significant exponential growth, games may use damping or “rubber-banding” mechanisms.
I discussed damping briefly in my previous article on player interaction, but here I will give it a fuller treatment. Whereas restraint mechanisms restrain players based on their absolute player state, damping mechanisms restrain players in ways which are based on the players’ relative states. Generally, players who are “ahead” are penalized, and/or players who are “behind” are rewarded.
Automatic Damping
Rewards and penalties based on player odds can come directly from the game rules. However, players’ true odds can’t be known in any modern board game, partially because these games haven’t been solved and partially because a players’ odds are dependent on the complex human behavior of them and their opponents. Therefore, games which damp players’ odds must do so using some aspect of players’ game states as a “proxy” for their odds. Players are rewarded or penalized if they are performing well or poorly according to this proxy. The more closely a proxy is correlated with players’ actual odds of winning, the more directly these damping mechanisms will constrain players’ odds.
Power Grid is a hugely exponential game. Players start the game with an income of 10 units and end the game with an income of around 150 units, because the rate of growth is high and the game is long (about 10-15 rounds). Furthermore, the impact of this income is great even compared to players endowments, which includes essentially a constant asset of $50 at the beginning of the game and a base rate of $10 income per turn. So with a high “k,” “c,” and “T,” this game has the potential to be highly volatile and thus have quickly diverging player odds.
However, Power Grid is a classic example of a game which uses automatic damping. In Power Grid, players are penalized according to their relative number of cities built. The player who has built the most cities loses initiative in buying resources and cities and is given a disadvantageous position in the auction of power plants. The player who has built the fewest cities gets first crack at purchasing resources and cities and has an advantageous position in the auction for power plants. Therefore Power Grid uses “cities built” as a proxy for player odds, which is reasonable because players cannot continue to grow economically without building more cities. Therefore, this proxy allows players to grow dramatically, but it constrains players so that it is more likely they will grow together.
As another example, Isle of Skye uses a very straightforward “catch-up” type of damping where players who are behind according to the proxy of “current victory points” gain the reward of extra gold income.
Correlation and Penalization
There are two properties of automatic damping mechanisms which are important to consider to understand their impact on the gameplay as well as evolution of player odds: first, the degree of correlation between the proxy and player odds, and second, the degree of penalization or rewards induced by the damping mechanism. For now I will simplify my writing by only talking about penalization, but the arguments apply similarly to rewards.
Let’s first assume the degree of penalization to be fixed and reasonable. Then the greater the correlation between the proxy and player odds, the more the penalization will result in damping of player odds. If the proxy is perfectly correlated with player odds, the penalization will act as a perfect damping mechanism but will not otherwise change the strategic nature of the game. This is of course impossible in any real game, therefore most damping mechanisms will be imperfect and thus will partially damp players odds and partially interfere with players’ strategic decision making. If a proxy has little or no correlation with player odds, then this mechanism cannot be considered a damping mechanism, but is better interpreted as part of the strategic fabric of the game. Or, when correlation between the proxy and player odds is negative, any penalization actually amplifies differences in player odds, and thus is a mechanism which serves to drive apart player odds. (Exponential growth mechanisms themselves could be interpreted this way).
Then, in order to discuss the impact of degree of penalization, let’s assume that the damping mechanism can be properly considered to be a damping mechanism, thus the correlation between the proxy and player odds is high but not perfect. Then, of course, no penalization will result in no damping, but as penalization increases, the advantage of having a high relative standing as measured by the proxy decreases, and thus player differences are damped. However, if penalization increase too much, players will actually become averse to success as measured by the proxy, and this can radically change the nature of the game (for better or worse). Thus, overall, the degree to which the damping mechanism interferes with a game depends on the interaction between the imperfection of the correlation of the proxy with player odds and the size of the penalization.
This can be observed in both Power Grid and Isle of Skye, wherein players will sometimes avoid success as measured by the proxy. In Isle of Skye, early game victory points can cost players a great amount of income throughout the course of the game, and therefore these points become assets with negative, rather than positive value. As players become more advanced at Power Grid, they will notice that economic development is sometimes counterproductive because of the penalization it will incur due to loss of initiative. To this extent, these “catch-up” mechanisms in Isle of Skye and Power Grid partially serve the purpose of damping but are also inseparable from the strategic fabric of the game. This is due to the imperfect correlation of the proxies with player odds as well as the high degree of penalization.
Agential Damping
Agential damping occurs whenever players have the agency to differentially impact other players’ odds. I discuss this principle at length in my previous article. To summarize, all modern games have some degree of targeted player interaction, but targeted player interaction has some emergent consequences, such as agential damping. Players will prefer to diminish the standing of those players with seemingly high standing, and this constitutes an agential penalization on relative player odds. All things being equal, more targeted player interaction will result in more damping, and thus in multiplayer games wherein players are unrestrained in their interactions, the damping will generally overwhelm any strategic decision making in the game. Thus most games limit players’ interactions using restrictions and incentives in order to control the amount of damping which arises from player interaction. However, the damping which arises from targeted player interaction can be used to counteract the divergence of player odds which results from factors such as exponential player growth.
For example in Risk, players grow exponentially but targeting is rampant. Therefore players who produce the most units should expect to be bullied into equilibrium with the other players, and will only win if either their opponents fail to act accordingly or their rate of growth surpasses the capacity of the agential damping.
In Small World, a modern cousin of Risk which does not have its exponential mechanisms, this agential damping is still present to some extent. Players who diligently keep track of how many victory points each player has collected so far should prefer, in some cases, to invade the territories of the player who is in the lead.
Whereas automatic damping relies on simple proxies for player odds, agential damping relies on players’ evaluations of others’ odds. In some cases, players may be able to relatively accurately evaluate other players’ odds, but in some cases they might poorly evaluate other players’ odds due to the complexity of the game or their own limitations as players. Worse yet, players may purposely target players who are actually behind. In all of these cases, players are engaging in various extents in kingmaking and abuse, which are concepts I define and discuss in my previous article.
Small World, Risk, Diplomacy, and in general multiplayer war games use targeted player interaction as a dominant damping mechanisms. Other games merely dabble in targeted player interaction; in Terraforming Mars, there are a handful of cards (usually “meteors”) which target other players. Terraforming Mars is unusual in the respect that while it includes “take-that” cards, their effects are relatively minor and the total effect of this limited targeted player interaction seems to be dominated by the variation in players’ growth.
My comments here are similar to my conclusions from my previous article; one of the most important directions in the evolution of modern multiplayer board games is the limitation of targeted player interaction. While technically it can serve to damp player odds in games with otherwise too-quickly divergent odds, it is one of the clumsiest ways to do so.
Solution 3: Variation Reduction
Recall that the problem of engine building games is that variation in player outcomes is amplified over time by player growth. The previous two solutions (restraint and damping) assume that variation in player outcomes exists and is fixed, and therefore these solutions prevent the divergence of player odds by, respectively, preventing the odds from being amplified by growth mechanisms and by correcting for people’s relative standings as the game progresses. This third solution, on the other hand, directly addresses the variation in player outcomes. The less players’ early game outcomes vary, the less these differences can be amplified by growth mechanisms and therefore the less player odds will diverge.
What causes player outcomes to vary? We could break it down in many different ways, but for the purpose of this article I will consider the quality of player outcomes to be the result of two independent factors: variability due to skill and variability due to luck. What exactly constitutes luck and skill is a complicated and unresolved question (which I write about in my article on luck, and which I will continue to write about as I refine my views). For now I will brush over the ambiguity involved in these edge cases and take advantage of whatever utility these categorizations seem to have.
Therefore, if games want to reduce the amount of variation in player outcomes, they can either reduce the amount of “luck” in the game, or they can reduce the amount of variability in player performances due to skill.
Variability due to Luck
There are many factors which contribute to the amount of luck in a game and in each individual outcome. In my article “Luck and Skill in Modern Board Games,” I co-opt Richard Garfield’s “Three Types of Luck” to discuss luck which arises from mechanical randomizers (Type I Luck), luck which arises from simultaneous decision making (Type II Luck) and luck which arises from decision making under intractable complexity (Type III Luck). In part to avoid the unease it causes some when I talk of Type II and Type III phenomena as “luck,” I will focus here on Type I luck, but the concepts should extend to the other types.
Games can manipulate the amount of variability in player outcomes using mechanical randomizers like dice and shuffled cards. The existence of mechanical randomizers does not necessitate a high amount of luck in a game; for instance, dice which are rolled frequently throughout the course of the game can be relatively equitable due to the convergence of their average results (as in Stone Age). Furthermore, luck in games is a force which counteracts the effect of skill on the outcome of a game, and therefore in general will decrease the divergence of player odds due to skill. However, if certain outcomes have a disproportionate impact on player odds, random perturbations of these outcomes will cause player odds to diverge quickly. It is precisely the case in engine building games that the importance of early game outcomes are amplified, therefore random perturbations in the quality of these outcomes is unlikely to be rectified later.
If the value of assets in games is highly disparate, games must allow players to choose between these assets rather than randomly assigning them. Because generally exponential games will have exponential, linear and constant-valued assets side by side, players must be allowed to choose the exponential assets early in the game. If a player is randomly deprived of exponential assets early in the game his odds will plummet too quickly.
Consider Suburbia, in which tiles may grant players income (of exponential value), reputation (of linear value) and immediate population (of constant value). To the extent that due to the randomization of the tiles, players may not see strong income-granting tiles early in the game, these players will fall rather behind. The game avoids this by having a relatively high density of income-granting tiles available in the early game, as well as having “backup” tiles which are always available, one of which grants players a unit of income.
Even more hazardous are games in which not only choices but assets are generated randomly. Consider two spiritually similar engine-building games: Settlers of Catan and Terra Mystica. In both games players build and upgrade buildings on a hex map which produce resources which can be used to build more buildings. Clearly, both games are highly exponential. However, in Settlers of Catan, buildings produce resources randomly whereas in Terra Mystica, income is perfectly predictable. Therefore, it is not surprising that Settlers of Catan relies heavily on an alternate solution for controlling the divergence of player odds: agential player interaction. Players who pull ahead are shunned by their trading partners and therefore are likely to stall somewhat due to their favorable relative standing. Of course, Catan is famously frustrating in cases where certain players struggle to build even one settlement while other players pull quickly ahead; this is one of the ways in which Catan shows its age relative to the most current games. On the other hand, Terra Mystica allows players to achieve any outcome they decide upon, as long as it is within their means (and with little impact from the possibly unpredictable actions of their opponents). This affords Terra Mystica the opportunity to be a longer game as well as well as the opportunity to do away with the agential damping that Catan requires.
Variability due to Skill
However, giving players reliable choices with predictable outcomes will only prevent the divergence of player odds if players actually make competent choices. For instance, some new players in Settlers of Catan will choose to build a road every time they find themselves with a wood and brick, and therefore fail to choose to build income-generating settlements. These players will find themselves in a hopeless situation rather quickly. In Dominion, a player who chooses to buy constant-valued estates early in the game will quickly find his deck irreparably inferior.
Some games embrace the likely economic domination of experienced players; I will write more about this in the section about Solution 5. However, in the spirit of modern board games which tend to attempt to cultivate a competitive experience even for new players, many games attempt to protect inexperienced players from sabotaging themselves. So whereas “luck reduction” reduces the divergence of player odds in engine building games by giving players fair access to assets of highly disparate value, this “skill gap reduction” method reduces the disparateness of the value of the available assets. Essentially, if a player is presented with a decision where each of her choices is of a similar albeit highly exponential value, this decision cannot impact her odds too dramatically. A softer version of this solution involves games demarking those assets which are meant for early game investment from those which are of constant-value so that players are unlikely to be tempted by constant-valued assets early in the game.
Consider Terra Mystica, in which players may choose what to build, but not whether to build. Generally, no matter how players spend their resources, they will somehow increase their income. There are few constant-valued assets which tempt inexperienced players into eschewing exponential assets. As an exception, when players build temples and sanctuaries, they must choose between favor tiles, some of which grant players income (of exponential value), others of which grant players points each round (of linear value), and some of which grant players a constant-valued three steps up a cult track. However, if anything, inexperienced players seem to be biased towards income-granting tiles and these constant-valued cult track tiles don’t tend to be too distracting.
Through the Ages is a game with quite quickly diverging player odds, but it does exhibit this variance reduction property to some extent. Although players can choose to invest in many different aspects of their civilization (food production, resource production, science production, or military), all of these areas have similarly exponential value. Therefore inexperienced players are more likely to fail to appropriately balance these exponential assets, but they aren’t like to fail to invest entirely. A main tension in the game involves the weighing of the linear asset of culture-point income against these other exponential assets.
Solution 4: Escalation
So far, we have examined the ways in which games prevent player odds from diverging by preventing players from growing too dramatically, by penalizing and rewarding players based on their standings, and by forcing players to achieve similarly valuable early outcomes. These solutions prevent player odds from diverging too quickly by manipulating the odds themselves, either directly or indirectly. This fourth solution instead prevents player odds from diverging too quickly by manipulating time. By pushing the main forces of odds divergence later into the game, we can reduce the amount of time that players have to wallow in hopelessness.
This solution has long been used by game shows to keep things competitive until the end of the episode. For example, in Family Feud, the points are doubled in the third round so that even if a team has lost both previous rounds, they can still recover. Similarly, Jeopardy escalates the stakes in the second round by doubling the value of the answers.
The underlying principle is that systematically increasing the variance of player outcomes over time damps diverging player odds. This is because in games where the only thing that matters is having more points than one’s opponents, high-variance outcomes benefit players who are behind. This is why in “push-your-luck” games players who are ahead should make conservative choices, whereas players who are behind should make risky choices.
Specifically, games must increase the component of the variance of player outcomes which is independent from their previous performance. Very often, games with player growth offer assets with high prices and high values late in the game for those players who have grown sufficiently as to afford them. This phenomenon is distinct from escalation, which refers to the introduction of late-game decisions which dominate the impact of early game decisions.
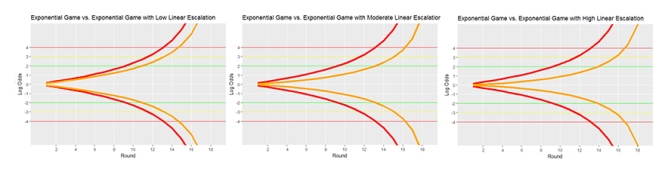
Let’s revisit our basic linear die-rolling game. Introducing an element of escalation damps the divergence of player odds. In the following plots, I compare the average odds divergence of a linear game (blue) with the odds divergence in linear games tempered by linear escalation, meaning that the variance of outcomes increases linearly over time.
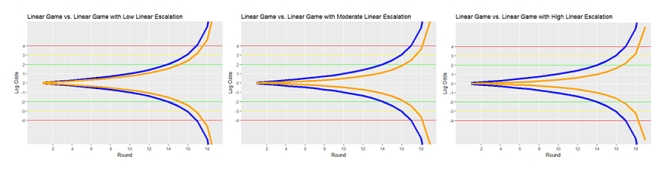
Thus we can see that the greater the degree of linear escalation relative to the initial variance of player outcomes, the longer it takes for odds to diverge. At most, linear escalation can entirely dominate the initial level of variation in player outcomes, resulting in something like the rightmost plot.
For a faster rate of escalation, we might consider exponential escalation. The following plots indicate why it may be inappropriate to apply strong exponential escalation to a linear game.
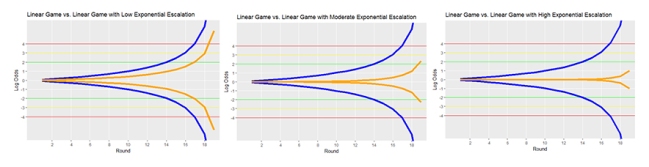
High exponential escalation will eventually completely dominate the importance of early game decisions in a linear game, so that only the last turns really matter.
A more common situation may be exponential games (red) which are mitigated by linear escalation. Eventually, exponential player growth will overwhelm the growth of the variance of player outcomes, but for any given game length some linear escalation regime can help restrain the divergence of player odds.
In fact, the exponential growth exhibited by engine-building games can be fully counterbalanced by introducing a rate of escalation which is commensurate with the rate of growth. The following plot shows a linear game completely overlapping with an exponential game with equal exponential escalation.
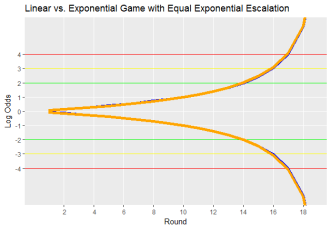Indeed, if the escalation takes exactly the same form as the player growth, the game will reduce to a linear game. For instance, in the Rabbit and Mule game, if Rabbits held by players doubled every round, but each round players could spend an action to take about twice as many Rabbits as they might have in the previous round, this game will be similar in character to a linear game.
The game which I find exhibits escalation most purely is Le Havre, in which players get an equal number of turns on which they take exactly one action, which involves either taking a stack of goods or using an action space (most of which grant players goods in some manner). To be clear, this game should not be characterized as a game of exponential growth, because assets are generally of constant value except for ships, which are of linear value. Because the value of ships dominates that of competing constant-valued assets, purchasing ships is essential (as pointed out in the rule book) and thus I believe Le Havre should be understood as a quadratic game.
The escalation in Le Havre arises elegantly from its basic mechanisms; action spaces of escalating value enter the game, and thus the accumulating resource piles are taken only when they become competitive with the value of the most current available action spaces. Thus the value of actions (and also the variability in the value of different outcomes) rises steadily as the game progresses. The escalation factor in Le Havre is linear but high: early in the game, players are thrilled to take an accumulation of 3 or 4 coins from the offering. By the end of the game, a pile of 8-12 coins is likely to go untouched.
Thus the quadratic player growth in Le Havre is counterbalanced by a high escalation factor. Players may perform somewhat better than other players in the first quarter of the game, but the losing player is still very much in competition because a strong performance later in the game can dominate his poor early performance. This type of natural escalation can be found in games which borrow Le Havre’s core mechanisms; Uwe Rosenberg’s follow up game Ora et Labora, as well as spiritually similar recent games such as The Colonists and Steam Works.
Escalation can generally be spotted in any game which has content which is divided into phases, such that endowments which players trade for acquisitions late in the game are more impactful. For instance, in 7 Wonders, cards are divided into three phases. This accomplishes two things; it facilitates the distribution of expensive cards late in the game which reward player growth, but it also facilitates the introduction of double-resource cards which can help players catch up from a lack of early game resources. This latter mechanism is a form of escalation.
Similarly, in Caylus, increasingly powerful action spaces are introduced as the game progresses. Thus late game actions are more important than early game actions, and this helps to constrain the divergence of player odds. However, to the extent that a player’s income (which does increase somewhat) facilitates her use of these spaces, the escalating actions actually reward growth and thus are partially restrained in their effectiveness in counteracting the divergence of player odds. This phenomenon is observed at the other end of the spectrum in Caylus’s spiritual successor, Agricola. In Agricola, action spaces also become somewhat more powerful as the game progresses, which may constitute some small degree of escalation. However, because player growth in the form of additional family members is such a dominating force in the game, players’ access to these late-game powerful actions is largely associated with their level of growth, and thus these action spaces may contribute more to the value of growth than to escalation. Thus in different contexts, the mechanism of “increasing action values” can either act as a form of escalation or conversely increase the impact of player growth.
A subtle form of escalation can be found in games with income phases which are broken up by increasing periods of actions. For instance, in a Feast for Odin, players collect income of exponential value seven times throughout the game. However, in each action phase, players are endowed with an additional action; players have six actions in the first action phase, then seven in the second, and so on. If we transform the way we look at time so that these income phases are evenly spaced, we can view the “action phases” as endowments of increasing value (and variance) over time. Thus the importance of early game action phases which gain players income generating assets is partially counterbalanced by the importance of late game action phases in which players have more actions.
Solution 5: Obfuscating or Embracing Player Elimination
In this article, I argue that modern board games embrace the desirable, exciting mechanism of exponential growth, but must somehow account for the divergence of player odds. The previous four solutions outline the mechanisms which games can use to manipulate players’ odds curves, either by manipulating the curves themselves (solutions 1-3) or by manipulating the time axis (solution 4). This final class of solutions (arguably non-solutions) involves allowing the quick divergence of player odds but somehow avoiding the negative player experience this may cause.
Obfuscating Diverging Player Odds
Diverging player odds can cause players to have a negative experience only if players are aware that their odds have diverged. Of course, in any unsolved game player odds are technically unknown, but players generally have a rough idea of their standing. Luckily, modern board games are often sufficiently intricate that the value of a player’s standing is rather opaque, especially to inexperienced players. Since these inexperienced players are likely to be the ones who fall quickly behind, their ignorance of their own hopelessness may ironically prevent them from despairing.
In many engine-building games, inexperienced players will tend to invest either too much in their engines or too little. If a player invests too little in his engine, he will find himself superficially “ahead” in terms of victory points despite the fact that he will eventually be overtaken by those players who have developed stronger engines. Thus, this inexperienced player may not realize how far behind he truly is until the end of the game. On the other hand, if a player invests too much in his engine, he will eventually notice that his score is low compared to other players, but he can still have hope that the the high power of his engine will rocket him to victory just in time. Thus, the opaque nature of engine-building as a mechanism can help to obfuscate the divergence in player odds in the eyes of inexperienced players.
Another way to obscure players standings’ is to veil blatant indicators of player standing. For instance, In Puerto Rico and Dominion, victory point assets are partially hidden so that even if their distribution can be known, new players are unlikely to keep close track of them.
Finally, many games are sufficiently deterministic that superficially small differences in player states are large factors in determining the outcome of the game, however, inexperienced players are unlikely to be depressed by these seemingly small discrepancies. Friedemann Friese speculates that the success of his Power Grid may have to do with the fact that players don’t tend to realize when they are in fact hopelessly behind because superficially, they have built a number of cities which is similar to the number built by their opponents.
De-emphasizing Competition
It is possible for players to be unaware that they are not seriously in contention to win a game, but it’s also possible that they don’t care. “Competitiveness” is more a property of a player than of the game, but games can reward players in ways that don’t require them to feel that they are in contention.
As I have argued in previous articles, one of the major innovations in modern multiplayer board games is the low degree of direct player interaction. Therefore, it is meaningful in some board games for players to “play against themselves” and simply try to do better each time. This would not be possible in Chess, a zero-sum game in which a player’s progression is totally dependent on the ways in which she interacts and competes with her opponent. It is nearly impossible to compare one’s achievements in a game of chess directly with that of a previous game. However, in A Feast for Odin, a player may be just as satisfied attempting to get a personal high score as getting a higher score than her opponent. As a related phenomenon, games which offer distinct “paths to victory” in the form of specialized strategies can cause players to feel as though they are playing separate games, thus removing them from the responsibility of direct competition.
Another related innovation in modern board games is the increased complexity of player states, and the thematic interpretation thereof. Board games which provide a generally interesting or pleasant experience outside of the ways in which it promotes competition may be able to get away with rather quickly diverging odds. For instance, in Agricola, a player may be proud of the farm he built at the end of the game because it is aesthetically pleasing albeit low-scoring. Similarly, in games like Terra Mystica, Suburbia, Carcassonne and Castles of the Mad King Ludwig, players build attractive physical entities, and doing so is somehow psychologically rewarding. Other thematic content such as art and story can give players purpose outside of competition.
Resignation and Elimination
In the absolute worst case, games which have rapidly diverging player odds, take a long time to play, and are overtly competitive should force or allow players to resign. This “solution” is rare among modern economic board games, and seems to mostly remain only as an artifact of older American combat-based games. Player elimination has become somewhat taboo in euro-style games, and can only be found either in light, short games like King of Tokyo or heavy war games. In Sid Meier’s Civilization: The Board Game, the game ends as soon as one player is eliminated. In Eclipse, player elimination is technically possible, but exceedingly rare.
In games where players can fall irreparably behind or are “logically” but not technically eliminated, they may be able to resign. Resignation is appropriate in two-player games, but it is rare that a multiplayer board game can accommodate resignation. A notable exception is Through the Ages, which is so heavily exponential and wherein players can suffer such traumatic outcomes that resignation is often necessary and thus is explicitly allowed by the rules.
Conclusion
In this article, I have defined engine building games as those in which the value of a player grows exponentially with the length of the game, T. I have introduced a way of visualizing the divergence of player odds and argued that exponential games should have player odds which diverge too quickly. Thus I have outlined five classes of solutions which address the problem of diverging player odds in engine building games.
I believe this framework should inform our analyses of modern board games. Growth characteristics are a fundamental property of games, and the archetypes of “linear,” “quadratic” and “exponential” games give powerful insights into their more complex real-life counterparts. By categorizing a game as “linear” or “exponential,” we can better understand the purpose of its mechanisms. This analysis can even inform the construction of games – for instance, it may streamline the process of designing a game to understand that introducing exponential assets may also warrant the introduction of mechanisms from one of these five classes of solutions.
In the future, I hope to expand on some of the more quantitative aspects of modeling player growth which I treated cursorily in this article. I also hope to do in-depth analyses of certain games with different growth characteristics mentioned in this article using the framework of diverging player odds and these five solutions.
The Board Game Snob 